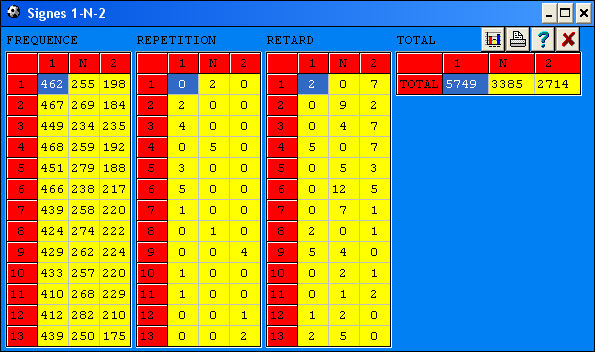
Sur L'état analytique on peut visualiser les éléments statistiques des signes 1,N,2 des grilles gagnantes d'où on prend les informations suivantes :

· Sorties des signes 1,N,2 : Présentation analytique des sorties de chaque signe. Le tableau indique le nombre de ses apparitions sur chaque match séparément (du 1er au 15e) par rapports aux grilles gagnantes enregistrées.
· Répétition de signes : Présente le nombre de fois qu'un signe est répété d'une grilles par rapport à une autre grille. Par exemple, si le signe 1 se répète 3 fois sur 1er matchs, on va voir apparaître le chiffre 3 dans la case correspondante. Quand le signe n'est pas sorti à la dernière grille gagnante, il n'y a pas de répétition de signe, il apparaît donc dans la case pour le match concerné le chiffre 0.
· Retard de signes : Présente le nombre de fois qu'un signe n'est pas sorti. Quand le signe n'est pas sorti durant 5 tirages consécutivement sur un match, ce signe sera en retard de 5 et dans la case correspondante au match concerné il apparaîtra le chiffre 5. Dans le cas il n'y a pas de retard, c'est à dire que le signe est sorti à la dernière grille gagnante, nous pourrons lire dans la case correspondante pour le match concerné le chiffre 0.
· Total des signes : ici on peut voir le nombre de fois que chacun des 3 signes est présenté sur l'ensemble des grilles gagnantes.
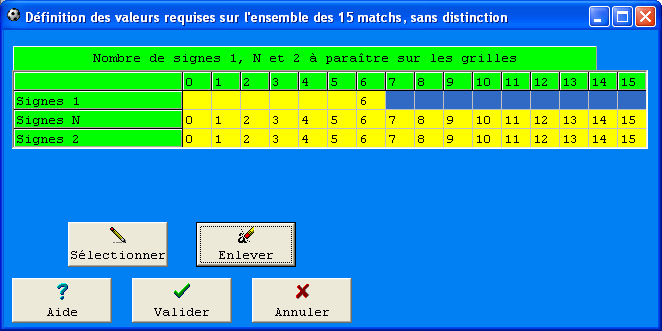
Dans le menu Analyser les 15 matchs, on peut indiquer au programme le nombre de signes que l'on veut voir apparaître sur chacune des grilles que l'on va construire. Ci-dessous, on demande 6 victoires à domicile sur l'ensemble des 15 matches.

Ici
les trois tableaux correspondent à chacun des 3 signes. Chaque tableau donne
pour chaque signe les trois informations suivantes:
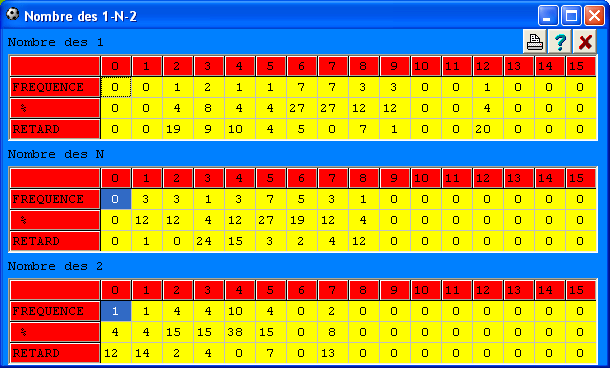
|
Fréquence
: Indique le nombre de signes sortis sur les grilles gagnantes (valeurs de
0 à 15 fois). On visualise pour chaque signe séparément la tendance des
grilles gagnantes enregistrées. Pourcentage : C'est la proportion des signes sortis sur les grilles gagnantes. Sur le tableau ci-dessus, on constate que 27% des grilles gagnantes contiennent 7 signes (N) et que 38% contiennent 4 signes (2). |
|
|
Retard : Représente le nombre de grilles gagnantes en retard selon le signe. Par exemple, en regardant le tableau ci-dessus, on constate que cela fait 24 tirages qu'une grille n'a pas contenu 3 signes (N). |

C'est le Schéma d'une grille réalisé en additionnant chaque signe distinctement.
Une Formule dérivée est l'expression raccourcie d'une grille comprenant 15 signes. Par exemple, la dérivée 8-3-4 signifie que dans la grille gagnante il y a 8 victoires à domicile (1), 3 matchs nuls (N) et 4 victoires à l'extérieur (2).
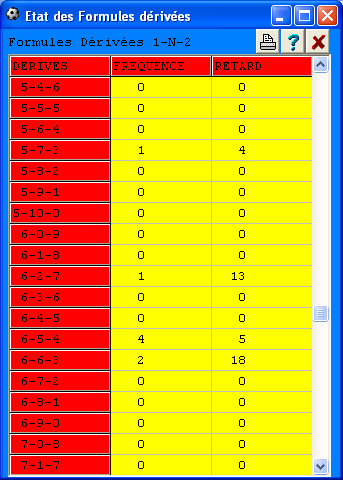 |
Dans l'Etat analytique du module Foot Stat, on peut visualiser toutes les dérivées possibles qu'une grille gagnante peut offrir, ainsi que leur sorties et leur retards. Il y a 136 possibilités différentes. Elles apparaissent dans la colonne de gauche. Pour chacune de ces Formules dérivées, on visualise ses sorties et ses retards. Nous distinguons deux sortes de Formules dérivées : Les formule dérivées 1-N-2 (Schéma d'une grille avec signes 1, N ou 2) et les formules dérivées A-B-C (Schéma d'une grille avec signes liés à l'ordre de préférence choisi). |

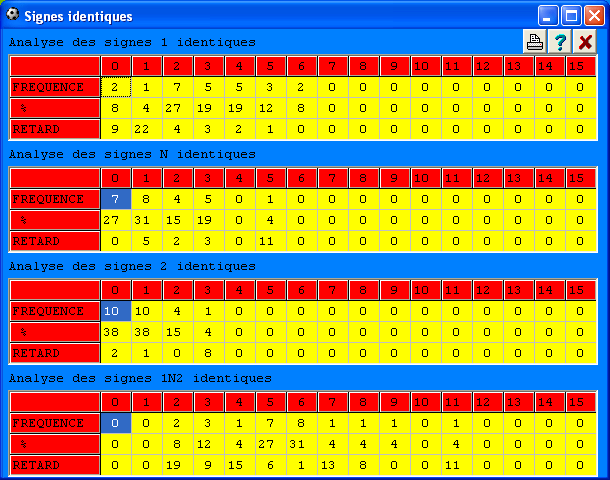
Par cette fonction, on définit le nombre de signes identiques, par rapport à la grille précédente, que l'on veut dans nos grilles. La fonction Signes identiques représente les signes qui se répètent d'un tirage à un autre à la même position (n° du match) dans la grille.
De la représentation des grilles gagnantes enregistrées ressort les signes communs entre deux grilles gagnantes qui se suivent. Le programme analyse le nombre de signes identiques d'une grille à une autre en considérant chaque match à la même position dans la grille.
On distingue le nombre de répétitions du (1) du (N) et du (2) et des 3 signes ensembles. Ce dernier n'est rien d'autre que la somme des répétitions des 3 signes.
Par exemple :
entre les deux grilles suivante, on constate 5 signes identiques (Matches 3, 5, 9, 11 et 15):
1 2 1 1 N N 1 N 2 1 1 N 2 1 1
N N 1 2 N 1 2 1 2 N 1 1 N 2 1
Dans le premier tableau ci-dessous, nous constatons que 7 grilles contiennent 2 signes (1) identiques soit 27% des grilles gagnantes !

On fixe le poids d'une grille en attribuant une valeur à chacun des signes 1 N 2 et en additionnant ces valeurs pour chacune des grilles gagnantes.
Par défaut, les signes 1 N 2 correspondent réciproquement aux valeurs 1, 0 et 2. Si on remplace chaque signe par la valeur équivalente et si on fait la somme des 15 nouvelles valeurs, on obtient le poids de la grille.
Le fait de cliquer sur une des valeurs comprises entre 0 et 30 et la faire disparaître de la case, enlève la possibilité qu'une grille du système ait un poids égal à cette valeur.
Exemple :La grille 1 1 N 2 2 1 N 1 1 N N 1 2 N N. Si on remplace les signes par les valeurs suivantes : Le signe 1 = 1, le signe N = 0 et Le signe 2 = 2, on obtient :1 + 1 + 0 + 2 + 2 + 1 + 0 + 1 + 1 + 0 + 0 + 1 + 2 + 0 + 0 = 12C'est le résultat de cette somme que l'on appelle le poids d'une grille.Le tableau Liste des tirages indique le poids qui correspond à chaque grille, ce poids est calculé avec les valeurs instruites par défaut. Le programme dès son origine utilise les valeurs suivantes :
Le signe 1 = 1
Le signe N = 0
Le signe 2 = 2Dans l'État Analytique , la colonne de gauche indique toutes les valeurs possibles qu'une grille gagnante puisse offrir, ainsi que leurs sorties et leurs retards. Pour chacune des valeurs possibles, on peut visualiser les sorties et les retards.
Le poids de la grille Signes ordonnés A-B-C, indique le poids de la grille après avoir hiérarchisé les signes par la fonction Priorité A B C. Par défaut, la valeur de A est de 1, la valeur B est de 2 et C a pour valeur 3.


On
parle d'alternance à chaque changement de signes. Chaque fois qu'il y a
dans la grille gagnante un changement de signes, on compte une alternance.
Une grille gagnante peut avoir de 0 à 14 alternance(s) ou changement(s) de
signes. Il y a 4 catégories d'alternances :
. alternances du 1 avec le N et du N avec le 1
. alternances du 1 avec le 2 et du 2 avec le 1
. alternances du N avec le 2 et du 2 avec le N
. alternance totale des trois.
Exemple: avec la grille gagnante : 1 1 2 N 1 N 2 N 1 2 2 1 N N N
Il y a quatre alternances du 1 N (ou N 1) : 1 1 2 N 1 N 2 N 1 2 2 1 N N N,
trois alternances du 1 2 (ou 2 1) : 1 1 2 N 1 N 2 N 1 2 2 1 N N N,
deux alternances du N 2 (ou 2 N) : 1 1 2 N 1 N 2 N 1 2 2 1 N N N
En somme nous distinguons 9
alternances différentes.
L'alternance globale est égale à : 4+3+2=
9.
Un fois votre base de données mise à jour, l'État analytique des alternances, du module Foot Stat, vous indique la tendance sur l'ensemble des grilles gagnantes. Le retard 0 pour les valeurs déjà sorties indique le nombre d'alternance correspondant à la dernière grille.

Le programme indique le nombre de groupes de signes consécutifs présents dans une grille. L'Etat analytique du module Foot Stat reprend toutes les valeurs sur l'ensemble des grilles gagnantes enregistrées dans la base de données choisie.
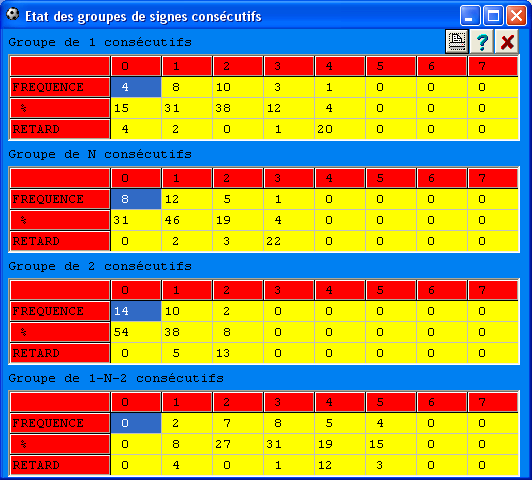
Il permet d'avoir une idée précise de la façon dont sont répartis les groupes de signes 1, N et 2 consécutifs selon les grilles enregistrées. Une grille comprendra un ou plusieurs groupe, à partir du moment où deux ou plusieurs signes semblables sont consécutifs. En conséquence, une grille gagnante peut avoir de 0 à 7 groupe(s) de signes.Important : notez que nous distinguons 4 groupes relatifs à l'analyse d'une grille :
1 Groupe de signes 1
2 Groupes de signes N
3 Groupes de signes 2
4 Groupes de signes indépendants.
Prenons l'exemple de la grille gagnante : 1 1 2 N N N 2 N 1 2 2 1 N 1 2.Si on compte les groupes on voit qu'il y a 1 groupe de deux signes 1 consécutifs , 1 groupe de trois signes N, 1 groupe de deux signes 2 et au total 3 groupes de signes indépendants formés par le {2 - 2 N 1 - 1 N 1 2}.
Par conséquent, comme on ne s'intéresse qu'aux signes consécutifs, on représentera cette grille selon la figure 1-1-1 et le total de cette figure, si on additionne les 3 valeurs qui la composent sera égale à : 1 + 1 + 1 = 3. Autre exemple : avec la grille gagnante : 1 1 2 N N 2 2 1 1 1 2 N N 1 2
Il y a deux groupes avec des signes 1 consécutifs (11 - 111), deux groupes avec des signes N consécutifs (NN - NN) et un groupe avec des signes 2 consécutifs(22). En fonction des signes 1-N-2, et pour représenter les signes consécutifs, on traduira cette grille gagnante comme cela: 2-2-1. Si on additionne les 3 valeurs qui la composent elle sera égale à 2 + 2 + 1 = 5.Le menu Requêtes & Conditions permet de sélectionner les valeurs requises:
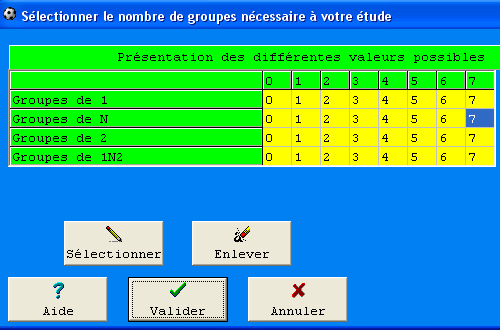

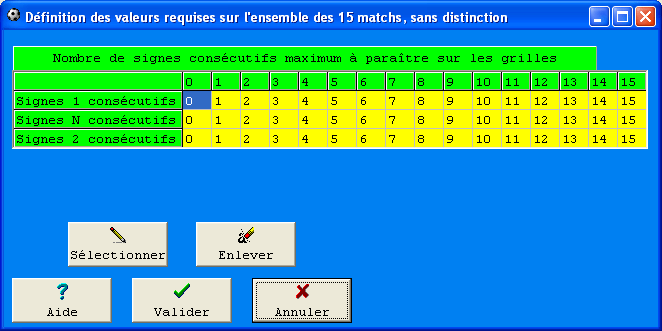
C'est le nombre maximum de signes consécutifs d'une grille. Si dans une grille gagnante, il n'y a pas plus de trois signes (1) consécutifs, et s'il n'y a pas plus de deux (N) consécutifs et aucun signe (2) consécutif, le Maximum de signes consécutifs de la grille gagnante sera représenté comme cela : 3-2-1
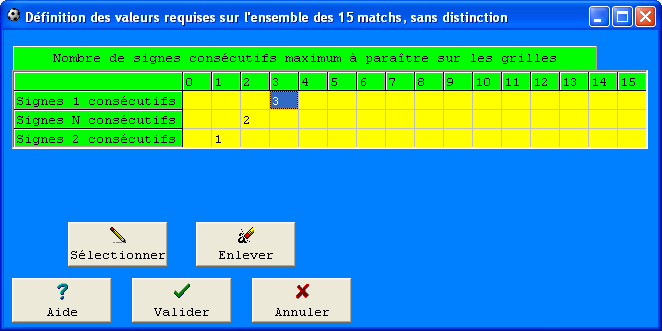
Vous l'avez compris, on ne prend que la plus grosse quantité de signes consécutifs. L'État analytique du module Foot Stat reprend toutes les valeurs sur l'ensemble des grilles gagnantes enregistrées dans la base de données choisie. De même que pour les autres tableaux analytiques, le retard 0 pour les valeurs des maximum des signes consécutifs, indique le Maximum de signes consécutifs correspondant à la dernière grille.
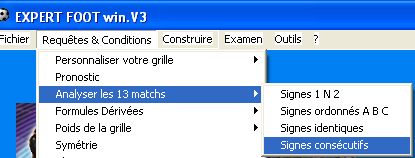

C'est le nombre des différentes paires de signes qui se trouvent dans une grille. Une grille peut avoir jusqu'à 9 différents doubles de signes. Voici pourquoi :(1-N-2)*(1-N-2)= 9 paires. De cette manière, on peut compter le nombre de paires de signes différents qui se trouvent dans une grille gagnante.
Pour bien comprendre comment le logiciel calcule chacun de ces groupes de signes, nous allons prendre un exemple. Admettons la grille N 1 1 1 1 2 2 N 1 1 2 N N N N
Celle-ci contient les Paires suivants {N1,11,11,12,22,2N,N1,11,12,2N,NN},soit 6 doubles différents suivants :{N1,11,12,22,2N,NN)
Analyse de toutes possibilités de Paires. Chacune des possibilités est analysée et l'Etat analytique du module Foot Stat vous présente les sorties et les retards des différentes paires offertes par chaque grille. Le retard 0 indique le nombre de paires différentes correspondant à la dernière grille.
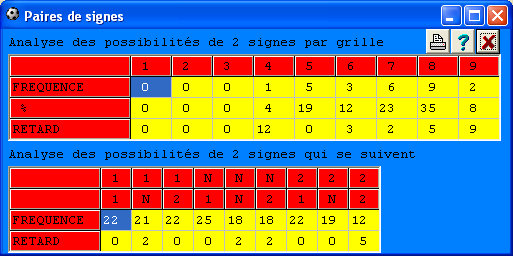

Le programme analyse de toutes les possibilités de Trios. Chacune des possibilités est analysée et l'Etat analytique du module Foot Stat vous présente les sorties et les retards des différents Trios offerts par chaque grille. Le retard 0, indique le nombre de Trios différents correspondant à la dernière grille.C'est le nombre de différents Trios de signes qui se trouvent dans une grille. Une grille gagnante peut avoir 27 différents Trios de signes,(1-N-2)*(1-N-2)*(1-N-2)= 27 Trios. De cette manière le logiciel répertorie à chaque grille le nombre des différents Trios de signes.Pour bien comprendre comment le logiciel calcule chacun de ces groupes de signes.
Par exemple. Admettons la grille N 1 1 1 1 2 2 N 1 1 2 N N 1 1 Celle-ci contient les 8 Trios différents suivants : {N11,111,112,122,22N,2N1,12N,2NN}

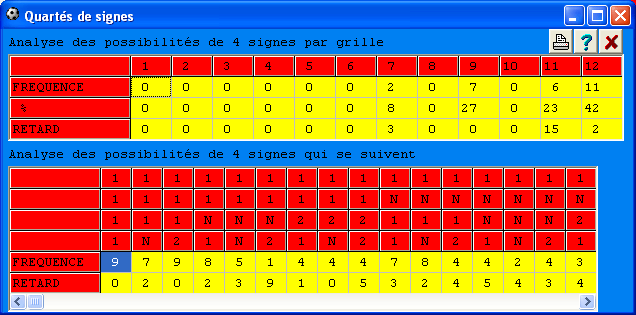
C'est le nombre de différents quartés de signes qui se trouvent dans une grille. Une grille gagnante peut avoir 81 différents quartés de signes,(1-N-2)*(1-N-2)*(1-N-2)*(1-N-2)= 81 combinaisons de quartés. On peut donc compter le nombre de quartés de signes différents qu'il y a dans une grille gagnante.Pour bien comprendre comment le logiciel calcule chacun de ses groupes de signes, nous allons prendre un exemple. Admettons la grille N 1 1 1 1 2 2 N 1 1 2 N N N N Elle contient les 10 quartés différents suivants :
{N111,1111,1112,1122,122N,22N1,2N11,N112,112N,12NN, 2NNN, NNNN).
Analyse de toutes possibilités de Quartés. Chacune des possibilités est analysée et l'État analytique du module Foot Stat vous présentent les sorties et les retards des différents Quartés offertes par chaque grille. Le retard 0, indique le nombre de Quartés différents correspondant à la dernière grille.

Somme Symétrie + Alternance + Groupes
C'est une analyse supplémentaire du programme. Elle repose sur une valeur statistique obtenue par addition des Symétrie + Alternance + groupes de signes consécutifs. Cela permet de classer les grilles selon le résultat de cette addition. Sachant que le maximum pour une symétrie est de 7, que le maximum possible pour une alternance est de 14 et que la valeur maximum pour un groupe de signes consécutifs est de 7, le maximum de la Somme Symétrie + Alternance + groupes est de 7 + 14 + 7 = 28.

